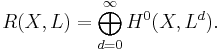Iitaka dimension

In algebraic geometry, the Iitaka dimension of a line bundle L on an algebraic variety X is the dimension of the image of the rational map to projective space determined by L. This is 1 less than the dimension of the ring

R(X, L) = \bigoplus_{d=0}^\infty H^0(X, L^d).

The Iitaka dimension of L is always less than or equal to the dimension of X. If L is not effective, then its Iitaka dimension is defined to be 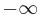-\infty (or sometimes −1).

Big line bundles

A line bundle is big if it is of maximal Iitaka dimension, that is, if its Iitaka dimension is equal to the dimension of the underlying variety. Bigness is a birational invariant: If f : Y → X is a birational morphism of varieties, and if L is a big line bundle on X, then f*L is a big line bundle on Y.

All ample line bundles are big.

Big line bundles need not determine birational isomorphisms of X with its image. For example, if C is a curve of genus 2, then the canonical bundle KC is big, but it determines a two-to-one covering, a morphism C to its image as canonical curve, which here is a rational normal curve.

Kodaira dimension

Main article: Kodaira dimension

The Iitaka dimension of the canonical bundle of a smooth variety is called its Kodaira dimension.

See also